Nice paper.
Recently 3blue1brown did a video on this topic with St...
**The problem of the brachistochrone was formally posed Johann Bern...
I built a program to send a ball down the brachistochrone and compa...
**Brachistochrone** from Ancient Greek βράχιστος χρόνος (brakhistos...
Galileo Galilei had considered the same problem much earlier. He ex...
The cycloid is the path described by a fixed point (figure 1: red p...
Equation $2.1$ reads: the total energy of the ball at any given hei...
Instead of determining the best curve analytically the author decid...
The goal is to find the shape $ds$ that connects point A to point B...
Integratio by parts is a theorem that relates the integral of a pro...
I think this implication only works if we know that $\frac{\partial...
This problem first introduced the notion of **calculus of variation...
## Finding the Cycloid
Here the author just introduces a change ...
Animation of a circle (dark blue) rolling along a straight line ge...
Think of particles in a uniform gravitational field (see different ...
If you are interested you can learn more about the isochronic pendu...
1
.
W
h
i
c
h
i
s
t
h
e
q
u
i
c
k
e
s
t
p
a
t
h
?
S
u
pp
o
s
e
t
h
e
r
e
i
s
a
n
i
n
c
li
n
e
s
u
c
h
a
s
t
h
a
t
s
h
o
w
n
i
n
F
i
g
u
r
e
1
.
W
h
e
n
aba
ll
r
o
ll
s
f
r
o
m
A
t
o
B
,
w
h
i
c
h
c
u
r
v
e
y
i
e
l
d
s
t
h
e
s
h
o
r
t
e
s
t
d
u
r
a
t
i
o
n
?
L
e
t
’
s
a
ss
u
m
e
t
h
a
t
w
e
h
a
v
e
t
h
r
ee
h
y
p
o
t
h
e
s
e
s
:
a
s
t
r
a
i
g
h
t
li
n
e
,
aq
u
a
d
r
a
t
i
c
,
a
n
d
a
c
y
c
l
o
i
d
.
T
h
e
s
h
o
r
t
e
s
t
p
a
t
h
f
r
o
m
A
t
o
B
i
s
t
h
e
s
t
r
a
i
g
h
t
li
n
e
,
s
o
o
n
e
m
i
g
h
tt
h
i
nk
t
h
a
tt
h
e
s
t
r
a
i
g
h
t
p
a
t
h
i
s
t
h
e
f
a
s
t
e
s
t
,
b
u
t
i
n
f
a
c
t
i
t
i
ss
u
r
p
r
i
s
i
n
g
l
y
s
l
o
w
.
I
t
’
s
b
e
tt
e
r
t
o
s
e
l
e
c
t
a
p
a
t
h
w
h
i
c
hh
a
s
a
d
o
w
n
w
a
r
dd
r
o
p
i
n
o
r
d
e
r
t
o
a
cc
e
l
e
r
a
t
e
t
h
e
ba
ll i
n
t
h
e
f
i
r
s
t
p
h
a
s
e
,
s
o
t
h
a
t
i
t
r
o
ll
s
q
u
i
c
k
l
y
.
T
h
e
ba
ll
a
rr
i
v
e
s
e
a
r
li
e
r
o
n
t
h
e
q
u
a
d
r
a
t
i
c
p
a
t
h
t
h
a
n
o
n
t
h
e
s
t
r
a
i
g
h
t
li
n
e
p
a
t
h
.
H
o
w
e
v
e
r
,
i
n
c
r
e
a
s
i
n
g
t
h
e
d
e
g
r
ee
o
f
t
h
e
f
un
c
t
i
o
n
c
a
u
s
e
s
t
h
e
ba
ll
t
o
t
r
a
v
e
l
m
o
r
e
s
l
o
w
l
y
o
n
t
h
e
f
l
a
t
s
e
c
t
i
o
n
.
I
t
i
ss
a
i
d
t
h
a
t
G
a
lil
e
o
(
1564
1642
)
f
i
r
s
t
p
r
e
s
e
n
t
e
d
t
h
i
s
p
r
o
b
l
e
m
.
I
t
i
s
a
l
s
o
kn
o
w
n
t
h
a
tt
h
e
c
y
-
c
l
o
i
d
i
s
t
h
e
c
u
r
v
e
w
h
i
c
h
y
i
e
l
d
s
t
h
e
q
u
i
c
k
e
s
t
d
e
s
c
e
n
t
.
T
h
i
s
t
i
m
e
I
w
ill
d
i
s
c
u
ss
t
h
i
s
p
r
o
b
l
e
m
,
w
h
i
c
h
m
a
y
b
e
h
a
n
d
l
e
d
un
d
e
r
t
h
e
f
i
e
l
d
kn
o
w
n
a
s
t
h
e
c
a
l
c
u
l
u
s
o
f
v
a
r
i
a
t
i
o
n
s
,
o
r
v
a
r
i
a
t
i
o
n
a
l
c
a
l
c
u
l
u
s
i
n
p
h
y
s
i
c
s
,
a
n
d
i
n
t
r
o
d
u
c
e
t
h
e
c
h
a
r
m
i
n
g
n
a
t
u
r
e
o
f
c
y
c
l
o
i
d
c
u
r
v
e
s
.
309
Y
u
t
a
k
a
N
i
s
h
i
y
a
m
a
O
s
a
k
a
K
e
i
d
a
i
R
o
n
s
hu
,
V
o
l
.
61
N
o
.
6
M
a
r
c
h
2011
T
h
e
B
r
a
c
h
i
s
t
o
c
h
r
o
n
e
C
u
r
v
e
:
T
h
e
P
r
o
b
l
e
m
o
f
Q
u
i
c
k
e
s
t
D
e
s
c
e
n
t
A
b
s
t
r
a
c
t
T
h
i
s
a
r
t
i
c
l
e
p
r
e
s
e
n
t
s
t
h
e
p
r
o
b
l
e
m
o
f
q
u
i
c
k
e
s
t
d
e
s
c
e
n
t
,
o
r
t
h
e
B
r
a
c
h
i
s
t
o
c
h
r
o
n
e
c
u
r
v
e
,
t
h
a
t
m
a
y
b
e
s
o
l
v
e
d
b
y
t
h
e
c
a
l
c
u
l
u
s
o
f
v
a
r
i
a
t
i
o
n
s
a
n
d
t
h
e
E
u
l
e
r
-
L
a
g
r
a
n
g
ee
q
u
a
t
i
o
n
.
T
h
e
c
y
c
l
o
i
d
i
s
t
h
e
q
u
i
c
k
e
s
t
c
u
r
v
e
a
n
d
a
l
s
o
h
a
s
t
h
e
p
r
o
p
e
r
t
y
o
f
i
s
o
c
h
r
o
n
i
s
m
b
y
w
h
i
c
h
H
u
y
g
e
n
s
i
m
p
r
o
v
e
d
o
n
G
a
lil
e
o
'
s
p
e
n
d
u
l
u
m
.
K
e
y
w
o
r
d
s
:
B
r
a
c
h
i
s
t
o
c
h
r
o
n
e
c
u
r
v
e
,
L
a
w
o
f
e
n
e
r
g
y
c
o
n
s
e
r
v
a
t
i
o
n
,
C
a
l
c
u
l
u
s
o
f
v
a
r
i
a
t
i
o
n
s
,
E
u
l
e
r
-
L
a
g
r
a
n
g
ee
q
u
a
t
i
o
n
,
C
y
c
l
o
i
d
,
I
s
o
c
h
r
o
n
i
s
m
,
H
u
y
g
e
n
s
'
s
p
e
n
d
u
l
u
m
F
i
g
u
r
e
1
.
W
h
i
c
h
p
a
t
h
y
i
e
l
d
s
t
h
e
s
h
o
r
t
e
s
t
d
u
r
a
t
i
o
n
?
A
B
2
.
M
o
d
e
l
c
o
n
s
t
r
u
c
t
i
o
n
a
n
d
nu
m
e
r
i
c
a
l
c
o
m
p
u
t
a
t
i
o
n
B
e
f
o
r
e
o
b
t
a
i
n
i
n
g
t
h
e
f
o
r
m
o
f
t
h
e
c
u
r
v
e
a
n
a
l
y
t
i
c
a
ll
y
,
l
e
t
’
s
t
r
y
s
o
m
e
nu
m
e
r
i
c
a
l
c
a
l
c
u
l
a
t
i
o
n
s
i
n
o
r
d
e
r
t
o
g
a
i
n
a
r
o
u
g
hun
d
e
r
s
t
a
n
d
i
n
g
o
f
t
h
e
p
r
o
b
l
e
m
.
I
c
a
l
c
u
l
a
t
e
d
t
h
e
a
rr
i
v
a
l
t
i
m
e
f
o
r
s
e
v
e
r
a
l
d
i
f
-
f
e
r
e
n
t
c
u
r
v
e
s
o
n
a
c
o
m
p
u
t
e
r
u
s
i
n
g
s
o
m
e
s
p
r
e
a
d
s
h
ee
t
s
o
f
t
w
a
r
e
.
U
s
i
n
g
t
h
e
c
oo
r
d
i
n
a
t
e
f
r
a
m
e
s
h
o
w
n
i
n
F
i
g
u
r
e
2
,
t
h
e
ba
ll
w
a
s
a
ss
u
m
e
d
t
o
r
o
ll
f
r
o
m
a
p
o
i
n
t
a
t
a
h
e
i
g
h
t
o
f
.
T
h
e
o
n
l
y
f
o
r
c
e
a
c
t
i
n
g
o
n
t
h
e
ba
ll i
s
t
h
e
f
o
r
c
e
d
u
e
t
o
g
r
a
v
i
t
y
,
,
a
n
d
f
r
o
m
t
h
e
l
a
w
o
f
e
n
e
r
g
y
c
o
n
s
e
r
v
a
t
i
o
n
,
t
h
e
s
u
m
o
f
t
h
e
p
o
t
e
n
t
i
a
l
e
n
e
r
g
y
a
n
d
t
h
e
k
i
n
e
t
i
c
e
n
e
r
g
y
i
s
c
o
n
s
t
a
n
t
,
s
o
w
h
e
n
t
h
e
ba
ll i
s
a
t
a
h
e
i
g
h
t
o
f
,
t
h
e
s
p
ee
d
m
a
y
b
e
o
b
t
a
i
n
e
d
a
s
f
o
ll
o
w
s
.
W
h
e
n
t
h
e
s
h
a
p
e
o
f
t
h
e
c
u
r
v
e
i
s
f
i
x
e
d
,
t
h
e
i
n
f
i
n
i
t
e
s
i
m
a
l
d
i
s
t
a
n
c
e
m
a
y
b
e
f
o
un
d
,
a
n
dd
i
v
i
d
i
n
g
t
h
i
s
b
y
t
h
e
v
e
l
o
c
i
t
y
y
i
e
l
d
s
t
h
e
i
n
f
i
n
i
t
e
s
i
m
a
l
d
u
r
a
t
i
o
n
.
I
f
a
n
i
n
f
i
n
i
t
e
s
i
m
a
l
d
u
r
a
t
i
o
n
s
u
c
h
a
s
t
h
i
s
i
s
i
n
t
e
g
r
a
t
e
d
,
t
h
e
r
e
s
u
l
t
i
s
t
h
e
t
i
m
e
un
t
il
a
rr
i
v
a
l
.
A
p
i
e
c
e
w
i
s
e
c
u
r
v
e
w
i
t
h
100
d
i
v
i
s
i
o
n
s
,
a
h
e
i
g
h
t
o
f
2
m
e
t
e
r
s
a
n
d
a
w
i
d
t
h
o
f
(=
3
.
14
)
m
e
t
e
r
s
w
a
s
u
s
e
d
t
o
p
r
o
d
u
c
e
nu
m
e
r
i
c
a
l
d
a
t
a
.
T
h
e
r
e
s
u
l
t
s
r
e
v
e
a
l
e
d
a
n
a
rr
i
v
a
l
t
i
m
e
o
f
1
.
189
s
f
o
r
t
h
e
s
t
r
a
i
g
h
t
li
n
e
,
1
.
046
s
f
o
r
t
h
e
q
u
a
d
r
a
t
i
c
,
1
.
019
s
f
o
r
a
c
u
b
i
cc
u
r
v
e
,
1
.
007
s
f
o
r
a
n
e
lli
p
s
e
a
n
d
1
.
003
s
f
o
r
t
h
e
c
y
c
l
o
i
d
.
T
h
e
s
t
r
a
i
g
h
t
li
n
e
w
a
s
t
h
e
s
l
o
w
e
s
t
,
a
n
d
t
h
e
c
u
r
v
e
d
li
n
e
w
a
s
t
h
e
q
u
i
c
k
e
s
t
.
T
h
e
d
i
f
-
f
e
r
e
n
c
e
b
e
t
w
ee
n
t
h
ee
lli
p
s
e
a
n
d
t
h
e
c
y
c
l
o
i
d
w
a
ss
li
g
h
t
,
b
e
i
n
g
o
n
l
y
0
.
004
s
.
T
h
e
a
rr
i
v
a
l
t
i
m
e
s
w
e
r
e
c
o
n
f
i
r
m
e
d
w
i
t
h
a
c
o
m
p
u
t
e
r
,
b
u
tt
h
i
s
l
a
c
k
s
a
s
e
n
s
e
o
f
r
e
a
li
t
y
,
w
h
i
c
h
m
a
d
e
m
e
w
a
n
tt
o
b
u
il
d
a
n
a
c
t
u
a
l
m
o
d
e
l
.
I
w
a
n
t
e
d
t
o
m
a
k
e
a
l
a
r
g
e
m
o
d
e
l
,
b
u
t
c
o
n
s
i
d
e
r
i
n
g
t
h
e
c
o
s
t
o
f
c
o
n
s
t
r
u
c
t
i
o
n
a
n
d
s
t
o
r
a
g
e
I
c
o
n
s
i
d
e
r
e
d
a
c
u
t
-
d
o
w
n
m
o
d
e
l
.
I
f
o
un
d
s
o
m
e
p
l
y
w
oo
d
w
i
t
h
h
o
r
i
z
o
n
t
a
l
a
n
d
v
e
r
t
i
c
a
l
d
i
m
e
n
s
i
o
n
s
o
f
30
×
45
c
m
i
n
a
D
I
Y
s
t
o
r
e
.
T
h
e
b
l
o
c
k
w
a
s
1
.
2
c
m
t
h
i
c
k
,
310
O
s
a
k
a
K
e
i
d
a
i
R
o
n
s
h
u
,
V
o
l
.
61
N
o
.
6
F
i
g
u
r
e
2
.
G
r
a
v
i
t
y
i
s
t
h
e
o
n
l
y
e
x
t
e
r
n
a
l
f
o
r
c
e
mg
O
y
x
0
y
a
n
d
s
i
n
c
e
p
a
c
h
i
n
k
o
ba
ll
s
(
u
s
e
d
i
n
t
h
e
p
o
p
u
l
a
r
J
a
p
a
n
e
s
e
v
e
r
s
i
o
n
o
f
p
i
n
ba
ll
)
a
r
e
1
.
1
c
m
i
n
d
i
a
m
e
-
t
e
r
,
t
h
i
s
w
a
ss
u
ff
i
c
i
e
n
t
.
O
n
t
h
e
c
o
m
p
u
t
e
r
,
t
h
e
t
i
m
e
f
o
r
t
h
e
s
t
r
a
i
g
h
t
li
n
e
w
a
s
0
.
445
s
,
f
o
r
t
h
e
q
u
a
d
-
r
a
t
i
c
i
t
w
a
s
0
.
391
s
,
a
n
d
f
o
r
t
h
e
c
y
c
l
o
i
d
i
t
w
a
s
0
.
375
s
.
P
e
r
f
o
r
m
i
n
g
t
h
e
s
ee
x
p
e
r
i
m
e
n
t
s
i
n
r
e
a
li
t
y
,
t
h
e
d
i
ff
e
r
e
n
c
e
b
e
t
w
ee
n
t
h
e
c
y
c
l
o
i
d
a
n
d
t
h
e
s
t
r
a
i
g
h
t
li
n
e
w
a
s
c
l
e
a
r
,
b
u
tt
h
e
d
i
ff
e
r
e
n
c
e
b
e
t
w
ee
n
t
h
e
c
y
c
l
o
i
d
a
n
d
t
h
e
q
u
a
d
r
a
t
i
c
r
e
q
u
i
r
e
d
a
pp
r
o
p
r
i
a
t
e
c
a
u
t
i
o
n
.
T
h
e
d
i
ff
e
r
e
n
c
e
i
n
a
rr
i
v
a
l
t
i
m
e
s
c
o
r
-
r
e
s
p
o
n
d
e
d
t
o
t
h
o
s
e
f
o
r
a
s
i
n
g
l
e
p
a
c
h
i
n
k
o
ba
ll
.
3
.
T
h
e
c
a
l
c
u
l
u
s
o
f
v
a
r
i
a
t
i
o
n
s
a
n
d
f
un
c
t
i
o
n
a
li
n
t
e
g
r
a
l
s
T
h
e
nu
m
e
r
i
c
a
l
c
a
l
c
u
l
a
t
i
o
n
s
ab
o
v
e
w
e
r
e
m
a
d
e
a
f
t
e
r
t
h
e
f
o
r
m
o
f
t
h
e
c
u
r
v
e
w
a
s
kn
o
w
n
,
b
u
t
l
e
t
’
s
t
h
i
nk
ab
o
u
tt
h
e
p
r
o
b
l
e
m
o
f
m
i
n
i
m
i
z
i
n
g
t
h
e
a
rr
i
v
a
l
t
i
m
e
i
n
t
h
e
c
a
s
e
t
h
a
tt
h
e
f
o
r
m
o
f
t
h
e
c
u
r
v
e
i
s
n
o
t
kn
o
w
n
.
L
e
t
u
s
d
e
n
o
t
e
t
h
e
s
t
a
r
t
i
n
g
a
n
d
f
i
n
a
ll
o
c
a
t
i
o
n
s
b
y
a
n
d
r
e
s
p
e
c
t
i
v
e
l
y
.
T
h
e
i
n
t
e
-
g
r
a
l
f
r
o
m
t
h
e
t
i
m
e
-
s
t
e
p
w
h
e
n
t
h
e
ba
ll i
s
a
tt
h
e
s
t
a
r
t
i
n
g
l
o
c
a
t
i
o
n
,
,
a
n
d
t
h
e
t
i
m
e
-
s
t
e
p
o
f
a
rr
i
v
a
l
,
,
i
s
t
h
e
d
u
r
a
t
i
o
n
o
f
m
o
t
i
o
n
,
.
L
e
t
u
s
i
n
v
e
s
t
i
g
a
t
e
t
h
ee
x
p
r
e
ss
i
o
n
o
f
t
h
i
s
u
s
i
n
g
a
n
d
.
I
f
t
h
e
i
n
f
i
n
i
t
e
s
i
m
a
l
e
l
e
m
e
n
t
i
s
t
a
k
e
n
a
s
,
t
h
e
n
t
h
e
f
o
ll
o
w
i
n
g
r
e
l
a
t
i
o
n
s
h
i
p
m
a
y
b
ee
s
t
ab
li
s
h
e
d
b
y
P
y
t
h
a
g
o
r
a
s
’
t
h
e
o
r
e
m
.
T
h
e
s
p
ee
d
o
f
t
h
e
ba
ll
,
,
m
a
y
b
e
f
o
un
d
b
y
t
a
k
i
n
g
t
h
e
t
i
m
e
d
e
r
i
v
a
t
i
v
e
o
f
t
h
e
d
i
s
t
a
n
c
e
a
l
o
n
g
t
h
e
c
u
r
v
e
.
T
h
i
s
m
a
y
b
e
w
r
i
tt
e
n
a
s
f
o
ll
o
w
s
.
E
q
u
a
t
i
o
n
(
3
.
1
)
m
a
y
b
e
r
e
w
r
i
tt
e
n
a
s
f
o
ll
o
w
s
,
u
s
i
n
g
E
q
u
a
t
i
o
n
s
(
3
.
2
)
a
n
d
(
3
.
3
)
.
I
f
t
h
e
c
oo
r
d
i
n
a
t
e
i
s
t
a
k
e
n
a
s
b
e
i
n
g
i
n
t
h
e
d
o
w
n
w
a
r
d
s
d
i
r
e
c
t
i
o
n
,
t
h
e
n
t
h
e
d
i
s
t
a
n
c
e
f
a
ll
e
n
,
,
a
n
d
t
h
e
s
p
ee
d
,
,
m
u
s
t
o
b
e
y
t
h
e
p
r
i
n
c
i
p
l
e
o
f
e
n
e
r
g
y
c
o
n
s
e
r
v
a
t
i
o
n
s
o
t
h
ee
q
u
a
t
i
o
n
i
ss
a
t
i
s
f
i
e
d
.
R
e
a
rr
a
n
g
i
n
g
y
i
e
l
d
s
,
S
u
b
s
t
i
t
u
t
i
n
g
t
h
i
s
i
n
t
o
E
q
u
a
t
i
o
n
(
3
.
4
)
,
a
n
d
w
r
i
t
i
n
g
f
o
r
y
i
e
l
d
s
t
h
e
f
o
ll
o
w
i
n
g
e
q
u
a
t
i
o
n
.
H
o
w
s
h
o
u
l
d
o
n
e
g
o
ab
o
u
t
m
i
n
i
m
i
z
i
n
g
a
cc
o
r
d
i
n
g
t
o
t
h
i
s
e
q
u
a
t
i
o
n
?
T
h
e
s
e
l
e
c
t
i
o
n
o
f
t
h
e
i
n
t
e
g
r
a
n
d
T
h
e
B
r
a
c
h
i
s
t
o
c
h
r
o
n
e
C
u
r
v
e
:
T
h
e
P
r
o
b
l
e
m
o
f
Q
u
i
c
k
e
s
t
D
e
s
c
e
n
t
311
i
n
o
r
d
e
r
t
o
m
i
n
i
m
i
z
e
i
s
a
p
r
o
b
l
e
m
i
n
t
h
e
c
a
l
c
u
l
u
s
o
f
v
a
r
i
a
t
i
o
n
s
.
4
.
T
h
e
E
u
l
e
r
-
L
a
g
r
a
n
g
ee
q
u
a
t
i
o
n
N
o
w
,
g
i
v
e
n
a
f
un
c
t
i
o
n
,
l
e
t
’
s
t
h
i
nk
ab
o
u
tt
h
e
p
r
o
b
l
e
m
o
ff
i
n
d
i
n
g
t
h
ee
x
t
r
e
m
a
l
v
a
l
u
e
o
f
t
h
e
i
n
t
e
g
r
a
l
,
b
y
s
e
tt
i
n
g
t
h
e
f
un
c
t
i
o
n
.
i
s
c
a
ll
e
d
a
f
un
c
t
i
o
n
a
l
.
T
h
i
s
e
x
p
r
e
ss
e
s
t
h
e
m
e
a
n
i
n
g
t
h
a
t
,
i
n
c
o
m
-
p
a
r
i
s
o
n
t
o
a
n
o
r
m
a
l
f
un
c
t
i
o
n
,
i
t
i
s
a
“
f
un
c
t
i
o
n
o
f
a
f
un
c
t
i
o
n
”
.
S
u
pp
o
s
e
w
e
h
a
v
e
a
f
un
c
t
i
o
n
w
h
i
c
h
i
ss
li
g
h
t
l
y
o
ff
s
e
t
f
r
o
m
,
t
h
e
f
un
c
t
i
o
n
w
e
a
r
e
s
ee
k
i
n
g
,
I
t
s
i
n
t
e
g
r
a
li
s
C
o
n
s
i
d
e
r
t
h
e
c
o
n
d
i
t
i
o
n
a
cc
o
r
d
i
n
g
t
o
w
h
i
c
h
i
tt
a
k
e
s
i
t
s
e
x
t
r
e
m
e
v
a
l
u
e
,
a
n
d
b
o
t
h
d
e
p
e
n
d
o
n
.
B
e
a
r
i
n
g
i
n
m
i
n
d
t
h
a
t
a
n
d
,
a
n
d
t
a
k
i
n
g
t
h
e
d
e
r
i
v
a
t
i
v
e
y
i
e
l
d
s
I
n
t
e
g
r
a
t
i
n
g
t
h
e
s
e
c
o
n
d
t
e
r
m
o
n
t
h
e
r
i
g
h
t
h
a
n
d
s
i
d
e
b
y
p
a
r
t
s
y
i
e
l
d
s
F
o
r
a
n
d
,
s
o
t
h
e
f
i
r
s
tt
e
r
m
o
n
t
h
e
r
i
g
h
t
h
a
n
d
s
i
d
e
o
f
t
h
i
s
e
q
u
a
t
i
o
n
i
s
z
e
r
o
.
T
h
e
c
o
n
-
d
i
t
i
o
n
f
o
r
t
h
ee
x
t
r
e
m
a
l
v
a
l
u
e
t
hu
s
b
e
c
o
m
e
s
S
i
n
c
e
i
s
a
r
b
i
t
r
a
r
y
,
t
h
e
f
o
ll
o
w
i
n
g
c
o
n
d
i
t
i
o
n
d
e
t
e
r
m
i
n
i
n
g
m
a
y
b
e
o
b
t
a
i
n
e
d
.
T
h
i
s
f
o
r
m
u
l
a
i
s
kn
o
w
n
a
s
E
u
l
e
r
’
s
e
q
u
a
t
i
o
n
,
o
r
a
l
t
e
r
n
a
t
i
v
e
l
y
t
h
e
E
u
l
e
r
-
L
a
g
r
a
n
g
ee
q
u
a
t
i
o
n
.
T
h
e
c
a
l
c
u
l
u
s
o
f
v
a
r
i
a
t
i
o
n
s
o
r
i
g
i
n
a
t
e
s
i
n
F
e
r
m
a
t
’
s
p
r
i
n
c
i
p
l
e
w
h
i
c
h
e
x
p
r
e
ss
e
s
h
o
w
t
h
e
p
a
t
h
o
f
ab
e
a
m
o
f
li
g
h
t
v
a
r
i
e
s
a
s
i
t
p
a
ss
e
s
t
h
r
o
u
g
h
m
e
d
i
a
w
i
t
h
d
i
ff
e
r
e
n
t
r
e
f
r
a
c
t
i
v
e
i
n
d
i
c
e
s
.
T
h
i
s
o
p
e
r
a
t
e
s
a
cc
o
r
d
-
i
n
g
t
o
t
h
e
p
r
i
n
c
i
p
l
e
t
h
a
tt
h
e
p
a
t
h
i
ss
e
l
e
c
t
e
d
i
n
o
r
d
e
r
t
o
m
i
n
i
m
i
z
e
t
h
e
p
a
ss
a
g
e
t
i
m
e
.
5
.
S
o
l
v
i
n
g
E
u
l
e
r
’
s
e
q
u
a
t
i
o
n
N
o
w
t
h
e
n
,
m
a
y
b
e
s
u
b
s
t
i
t
u
t
e
d
i
n
t
o
t
h
e
E
u
l
e
r
-
L
a
g
r
a
n
g
ee
q
u
a
t
i
o
n
,
b
u
t
i
s
n
o
t
e
x
p
li
c
i
t
l
y
c
o
n
t
a
i
n
e
d
i
n
,
i
.
e
.,
i
t
i
s
a
f
un
c
t
i
o
n
o
f
a
n
d
a
l
o
n
e
.
T
h
e
312
O
s
a
k
a
K
e
i
d
a
i
R
o
n
s
h
u
,
V
o
l
.
61
N
o
.
6
f
o
ll
o
w
i
n
g
t
r
a
n
s
f
o
r
m
a
t
i
o
n
o
f
E
u
l
e
r
’
s
e
q
u
a
t
i
o
n
m
a
y
t
h
e
r
e
f
o
r
e
b
e
u
s
e
d
.
S
u
b
s
t
i
t
u
t
i
n
g
f
o
r
i
n
t
h
i
s
e
q
u
a
t
i
o
n
,
S
q
u
a
r
i
n
g
b
o
t
h
s
i
d
e
s
,
t
h
ee
q
u
a
t
i
o
n
m
a
y
b
e
r
e
a
rr
a
n
g
e
d
a
s
f
o
ll
o
w
s
.
S
i
n
c
e
t
h
e
r
i
g
h
t
h
a
n
d
s
i
d
e
i
s
c
o
n
s
t
a
n
t
,
s
o
w
e
m
a
y
w
r
i
t
e
i
t
a
s
2
A
.
E
q
u
a
t
i
o
n
(
5
.
3
)
i
s
r
e
a
rr
a
n
g
e
d
a
s
f
o
ll
o
w
s
.
T
h
e
d
o
m
a
i
n
o
f
t
h
e
c
u
r
v
e
i
s
t
a
k
e
n
a
s
T
h
e
i
n
i
t
i
a
l
c
o
n
d
i
t
i
o
n
i
s
t
a
k
e
n
a
s
w
h
e
n
.
A
tt
h
i
s
p
o
i
n
t
m
a
y
b
e
r
e
w
r
i
tt
e
n
a
s
t
h
e
f
o
ll
o
w
-
i
n
g
p
a
r
a
m
e
t
r
i
c
a
l
e
x
p
r
e
ss
i
o
nu
s
i
n
g
a
c
h
a
n
g
e
o
f
v
a
r
i
ab
l
e
.
T
h
i
s
c
h
a
n
g
e
o
f
v
a
r
i
ab
l
e (
5
.
6
)
m
a
y
s
ee
m
s
o
m
e
w
h
a
t
s
u
dd
e
n
.
R
a
t
h
e
r
t
h
a
n
d
e
t
e
r
m
i
n
i
n
g
t
h
e
n
a
-
t
u
r
e
o
f
t
h
e
f
un
c
t
i
o
n
a
cc
o
r
d
i
n
g
t
o
t
h
e
c
a
l
c
u
l
u
s
o
f
v
a
r
i
a
t
i
o
n
s
,
i
n
t
h
i
s
c
a
s
e
i
t
w
a
s
a
l
r
e
a
d
y
kn
o
w
n
t
h
a
tt
h
e
c
y
c
l
o
i
d
i
s
t
h
e
c
u
r
v
e
o
f
q
u
i
c
k
e
s
t
d
e
s
c
e
n
t
b
e
c
a
u
s
e
r
e
s
e
a
r
c
h
o
n
c
y
c
l
o
i
d
s
h
a
s
b
ee
n
d
e
v
e
l
-
o
p
i
n
g
f
o
r
a
c
o
n
s
i
d
e
r
ab
l
e
l
e
n
g
t
h
o
f
t
i
m
e
.
I
t
i
ss
u
ff
i
c
i
e
n
tt
o
un
d
e
r
s
t
a
n
d
t
h
a
tt
h
i
s
c
u
r
v
e
w
a
s
t
a
k
e
n
a
s
a
h
y
p
o
t
h
e
s
i
s
a
n
d
t
h
e
s
o
l
u
t
i
o
n
w
a
s
o
b
t
a
i
n
e
d
u
s
i
n
g
t
h
e
c
a
l
c
u
l
u
s
o
f
v
a
r
i
a
t
i
o
n
s
.
I
f
b
o
t
h
s
i
d
e
s
o
f
E
q
u
a
t
i
o
n
(
5
.
6
)
a
r
e
d
i
ff
e
r
e
n
t
i
a
t
e
d
t
h
e
n
t
h
e
r
e
s
u
l
t
i
s
a
s
f
o
ll
o
w
s
.
I
t
i
s
p
o
ss
i
b
l
e
r
e
w
r
i
t
e
E
q
u
a
t
i
o
n
(
5
.
7
)
u
s
i
n
g
t
h
e
p
a
r
a
m
e
t
r
i
c
e
x
p
r
e
ss
i
o
n
f
o
r
a
s
f
o
ll
o
w
s
.
T
h
i
s
c
a
n
b
e
w
r
i
tt
e
n
a
s
f
o
ll
o
w
s
,
b
y
m
u
l
t
i
p
l
y
i
n
g
b
o
t
h
s
i
d
e
s
b
y
.
T
h
e
r
e
l
a
t
i
o
n
s
h
i
p
b
e
t
w
ee
n
a
n
d
m
a
y
b
e
f
o
un
d
b
y
c
o
ll
a
t
i
n
g
E
q
u
a
t
i
o
n
s
(
5
.
7
)
a
n
d
(
5
.
9
)
,
a
n
d
e
li
m
i
n
a
t
i
n
g
.
I
n
t
e
g
r
a
t
i
n
g
b
o
t
h
s
i
d
e
s
,
T
h
e
B
r
a
c
h
i
s
t
o
c
h
r
o
n
e
C
u
r
v
e
:
T
h
e
P
r
o
b
l
e
m
o
f
Q
u
i
c
k
e
s
t
D
e
s
c
e
n
t
313
F
o
r
t
h
e
i
n
i
t
i
a
l
c
o
n
d
i
t
i
o
n
w
h
e
n
,
t
h
e
c
o
n
s
t
a
n
t
o
f
i
n
t
e
g
r
a
t
i
o
n
i
s
.
F
i
n
a
ll
y
,
t
h
e
p
a
r
a
m
e
t
r
i
c
e
x
p
r
e
ss
i
o
n
f
o
r
t
h
e
c
u
r
v
e
o
f
q
u
i
c
k
e
s
t
d
e
s
c
e
n
t
i
s
a
s
f
o
ll
o
w
s
.
6
.
T
h
e
c
y
c
l
o
i
d
A
c
y
c
l
o
i
d
m
a
y
b
ee
x
p
r
e
ss
e
d
a
s
t
h
e
t
r
a
j
e
c
t
o
r
y
o
f
a
p
o
i
n
t
f
i
x
e
d
o
n
t
h
e
c
i
r
c
u
m
f
e
r
e
n
c
e
o
f
a
c
i
r
c
l
e
w
i
t
h
r
a
d
i
u
s
,
w
h
e
n
t
h
e
c
i
r
c
l
e
r
o
ll
s
a
l
o
n
g
a
s
t
r
a
i
g
h
t
li
n
e
.
W
h
e
n
t
h
e
a
n
g
l
e
o
f
t
h
e
c
i
r
c
l
e
’
s
r
o
t
a
t
i
o
n
i
s
,
t
h
e
c
oo
r
d
i
n
a
t
e
s
o
n
t
h
e
c
u
r
v
e
a
r
e
a
s
f
o
ll
o
w
s
.
T
h
e
d
e
r
i
v
a
t
i
v
e
s
a
r
e
a
n
d
.
B
e
a
r
i
n
g
i
n
m
i
n
d
t
h
a
t
,
w
e
m
a
y
w
r
i
t
e
T
h
i
s
i
s
t
h
e
d
i
ff
e
r
e
n
t
i
a
l
e
q
u
a
t
i
o
n
o
f
t
h
e
c
y
c
l
o
i
d
,
a
n
d
i
t
s
h
o
u
l
d
b
e
n
o
t
e
d
t
h
a
t
i
t
i
s
e
q
u
i
v
a
l
e
n
tt
o
t
h
e
p
r
e
v
i
o
u
s
l
y
s
t
a
t
e
d
E
q
u
a
t
i
o
n
(
5
.
4
)
.
I
t
i
s
c
o
mm
o
n
f
o
r
t
h
ee
x
p
l
a
n
a
t
i
o
n
o
f
t
h
e
c
y
c
l
o
i
dg
i
v
e
n
i
nh
i
g
h
-
s
c
h
oo
l
m
a
t
h
e
m
a
t
i
c
s
t
e
x
t
b
oo
k
s
t
o
s
t
a
t
e
n
o
m
o
r
e
t
h
a
n
t
h
a
t
i
t
i
s
t
h
e
t
r
a
j
e
c
t
o
r
y
o
f
a
p
o
i
n
t
o
n
ab
i
-
c
y
c
l
e
w
h
ee
l
.
I
t
’
s
a
s
h
a
m
e
t
h
a
tt
h
ee
x
c
e
p
t
i
o
n
a
l
p
r
o
p
e
r
t
y
t
h
a
t
i
t
i
s
t
h
e
c
u
r
v
e
o
f
q
u
i
c
k
e
s
t
d
e
s
c
e
n
t
i
s
r
a
r
e
l
y
e
x
p
l
a
i
n
e
d
.
7
.
I
s
o
c
h
r
o
n
i
s
m
I
t
w
a
s
G
a
lil
e
o
w
h
o
d
i
s
c
o
v
e
r
e
d
t
h
e
i
s
o
c
h
r
o
s
i
s
m
o
f
p
e
n
d
u
l
u
m
s
.
S
u
pp
o
s
i
n
g
t
h
e
l
e
n
g
t
h
o
f
a
g
i
v
e
n
p
e
n
d
u
l
u
m
i
s
,
t
h
e
g
r
a
v
i
t
a
t
i
o
n
a
l
c
o
n
s
t
a
n
t
i
s
,
a
n
d
t
h
ee
q
u
ili
b
r
i
u
m
p
o
i
n
t
o
f
t
h
e
p
e
n
d
u
l
u
m
i
s
a
t
t
h
e
o
r
i
g
i
n
,
t
h
e
n
w
h
e
n
t
h
e
s
w
i
n
g
a
n
g
l
e
o
f
t
h
e
p
e
n
d
u
l
u
m
i
s
,
t
h
ee
q
u
a
t
i
o
n
o
f
t
h
e
p
e
n
d
u
l
u
m
’
s
m
o
-
t
i
o
n
i
s
a
s
f
o
ll
o
w
s
.
H
y
p
o
t
h
e
s
i
z
i
n
g
t
h
a
t
w
h
e
n
t
h
e
a
n
g
l
e
o
f
s
w
i
n
g
i
ss
m
a
ll
,
,
t
h
ee
q
u
a
t
i
o
n
m
a
y
b
e
s
i
m
p
li
f
i
e
d
a
s
f
o
ll
o
w
s
.
314
O
s
a
k
a
K
e
i
d
a
i
R
o
n
s
h
u
,
V
o
l
.
61
N
o
.
6
A
B
F
i
g
u
r
e
3
.
T
h
e
c
y
c
l
o
i
d
T
h
e
p
e
r
i
o
d
i
s
I
e
x
p
l
a
i
n
e
d
t
h
a
tt
h
e
c
y
c
l
o
i
d
w
a
s
t
h
e
c
u
r
v
e
o
f
q
u
i
c
k
e
s
t
d
e
s
c
e
n
t
,
b
u
t
i
t
h
a
s
o
n
e
m
o
r
ee
x
c
e
p
-
t
i
o
n
a
l
p
r
o
p
e
r
t
y
,
i
t
i
s
i
s
o
c
h
r
o
n
i
c
.
W
h
e
t
h
e
r
aba
ll i
s
r
o
ll
e
d
f
r
o
m
t
h
e
p
o
i
n
t
A
s
h
o
w
n
i
n
F
i
g
u
r
e
4
,
o
r
f
r
o
m
t
h
e
i
n
t
e
r
m
e
d
i
a
t
e
p
o
i
n
t
C
,
t
h
e
t
i
m
e
t
a
k
e
n
t
o
a
rr
i
v
e
a
t
p
o
i
n
t
B
i
s
t
h
e
s
a
m
e
.
Q
u
e
s
t
i
o
n
1
P
r
o
v
e
t
h
a
t
f
o
r
ba
ll
s
p
l
a
c
e
d
o
n
a
c
y
c
l
o
i
d
c
u
r
v
e
,
e
v
e
n
i
f
t
h
e
i
r
p
o
s
i
t
i
o
n
s
d
i
ff
e
r
,
t
h
e
t
i
m
e
t
a
k
e
n
t
o
r
e
a
c
h
t
h
e
l
o
w
e
s
t
p
o
i
n
t
i
s
t
h
e
s
a
m
e
.
W
h
e
n
t
h
e
s
w
i
n
g
o
f
G
a
lil
e
o
’
s
p
e
n
d
u
l
u
m
g
r
o
w
s
l
a
r
g
e
,
t
h
e
i
s
o
c
h
r
o
n
i
s
m
b
r
e
a
k
s
d
o
w
n
a
n
d
t
h
e
c
y
c
l
e
t
i
m
e
g
r
o
w
s
l
o
n
g
e
r
.
I
f
t
h
e
p
e
n
d
u
l
u
mm
o
v
e
s
ba
c
k
a
n
d
f
o
r
t
h
o
n
a
c
y
c
l
o
i
d
,
i
s
o
c
h
r
o
n
i
s
m
s
h
o
u
l
d
b
e
s
a
t
i
s
f
i
e
d
.
H
u
y
g
e
n
s
(
1629
1695
)
i
m
p
l
e
m
e
n
t
e
d
a
n
i
s
o
c
h
r
o
n
i
c
p
e
n
d
u
l
u
m
a
s
f
o
ll
o
w
s
.
T
w
o
c
y
c
l
o
i
d
s
a
r
e
d
e
s
c
r
i
b
e
d
,
a
ss
h
o
w
n
i
n
F
i
g
u
r
e
5
.
W
h
e
n
a
r
o
p
e
o
f
l
e
n
g
t
h
(
t
h
e
l
e
n
g
t
h
o
f
t
h
e
c
y
c
l
o
i
d
c
u
r
v
e
i
s
)
w
i
t
h
p
o
i
n
t
a
t
i
t
s
c
e
n
t
e
r
i
s
p
u
ll
e
d
f
r
o
m
p
o
i
n
t
,
t
h
e
t
r
a
j
e
c
-
t
o
r
y
f
o
r
m
s
a
c
y
c
l
o
i
d
.
T
h
i
s
k
i
n
d
o
f
c
u
r
v
e
i
s
kn
o
w
n
a
s
a
n
i
n
v
o
l
u
t
i
o
n
.
Q
u
e
s
t
i
o
n
2
P
r
o
v
e
t
h
a
tt
h
e
c
y
c
l
o
i
d
’
s
i
n
v
o
l
u
t
i
o
n
i
s
i
n
d
ee
d
a
c
y
c
l
o
i
d
.
T
h
e
c
y
c
l
o
i
d
p
e
n
d
u
l
u
m
d
e
v
i
s
e
d
b
y
H
u
y
g
e
n
s
i
s
t
h
e
s
a
m
e
a
s
F
i
g
u
r
e
5
f
li
pp
e
d
v
e
r
t
i
c
a
ll
y
w
i
t
h
t
h
e
c
e
n
t
r
a
l
h
a
l
f
r
e
m
o
v
e
d
(
F
i
g
u
r
e
6
)
.
W
i
t
h
t
h
i
s
p
e
n
d
u
l
u
m
,
e
v
e
n
w
h
e
n
t
h
e
s
w
i
n
g
i
s
l
a
r
g
e
,
i
s
o
c
h
r
o
n
i
s
m
i
s
m
a
i
n
t
a
i
n
e
d
.
C
l
o
c
k
s
e
m
p
l
o
y
i
n
g
t
h
i
s
p
r
i
n
c
i
p
l
e
a
r
e
m
o
r
e
a
cc
u
r
a
t
e
t
h
a
n
G
a
lil
e
o
c
l
o
c
k
s
.
T
h
e
l
e
n
g
t
h
o
f
t
h
e
p
e
n
d
u
l
u
m
,
i
s
h
a
l
f
t
h
e
l
e
n
g
t
h
o
f
t
h
e
p
e
n
d
u
l
u
m
’
ss
w
i
n
g
c
y
c
l
e
,
.
T
h
e
p
e
r
i
o
d
,
i
s
T
h
e
B
r
a
c
h
i
s
t
o
c
h
r
o
n
e
C
u
r
v
e
:
T
h
e
P
r
o
b
l
e
m
o
f
Q
u
i
c
k
e
s
t
D
e
s
c
e
n
t
315
A
B
C
F
i
g
u
r
e
4
.
T
h
e
i
s
o
c
h
o
n
i
s
m
o
f
c
y
c
l
o
i
d
s
A
B
C
P
D
F
i
g
u
r
e
5
.
T
h
e
c
y
c
l
o
i
d
’
s
i
n
v
o
l
u
t
i
o
n
i
s
a
c
y
c
l
o
i
d
N
o
w
a
d
a
y
s
a
c
t
u
a
l
m
o
d
e
l
s
o
f
t
h
e
B
r
a
c
h
i
s
t
o
c
h
r
o
n
e
c
u
r
v
e
c
a
n
b
e
s
ee
n
o
n
l
y
i
n
s
c
i
e
n
c
e
m
u
s
e
u
m
s
.
B
u
t
w
e
s
h
o
u
l
d
n
o
t
f
o
r
g
e
tt
h
a
tt
h
e
p
r
o
b
l
e
m
o
f
q
u
i
c
k
e
s
t
d
e
s
c
e
n
t
m
a
t
h
e
m
a
t
i
c
a
ll
y
d
e
v
e
l
o
p
e
d
t
h
e
s
t
u
d
y
o
f
t
h
e
c
y
c
l
o
i
d
a
n
d
t
h
e
c
a
l
c
u
l
u
s
o
f
v
a
r
i
a
t
i
o
n
s
,
a
n
d
c
o
n
t
r
i
b
u
t
e
d
t
o
t
h
e
i
m
p
r
o
v
e
m
e
n
t
o
f
p
e
n
-
d
u
l
u
m
s
.
R
e
f
e
r
e
n
c
e
T
a
k
a
ku
w
a
,
S
.
(
2003
)
.
B
i
b
un
H
o
t
e
i
s
h
i
k
i
t
o
H
e
n
b
un
h
o
[
D
i
ff
e
r
e
n
t
i
a
l
e
q
u
a
t
i
o
n
s
a
n
d
t
h
e
c
a
l
c
u
l
u
s
o
f
v
a
r
i
a
-
t
i
o
n
s
]
,
T
o
k
y
o
:
K
y
o
r
i
t
s
u
.
316
O
s
a
k
a
K
e
i
d
a
i
R
o
n
s
h
u
,
V
o
l
.
61
N
o
.
6
F
i
g
u
r
e
6
.
H
u
y
g
e
n
s
’
s
p
e
n
d
u
l
u
m
Animation of a circle (dark blue) rolling along a straight line generating a cycloid (light blue).

The goal is to find the shape $ds$ that connects point A to point B that minimizes the arrival time. We know that the total time T can be written:
\begin{eqnarray*}
T = \int_{t_A}^{t_B}{dt}.
\end{eqnarray*}
Our goal is to find the curve that minimizes T. Read on to find out how we can obtain this result analytically.
Instead of determining the best curve analytically the author decides to create various shapes and solve the problem in a **computational way**. We can see that the **cycloid gives the shortest time** to go from point A to point B. Read further to understand how one can determine analatically that the cyclloid is the best solution to this problem.
If you are interested you can learn more about the isochronic pendulum here: [Sumit Kumar - Isochronic Pendulum](http://arxiv.org/pdf/1107.5664v1.pdf)
Here is a nice video showcasing the isochronic property of the cycloid: [Brachistochrone Race
](https://www.youtube.com/watch?v=Ib1TdgeYL4o "Brachistochrone Race")
Equation $2.1$ reads: the total energy of the ball at any given height $y$ (right side) will always be equal to the initial energy of the ball at $y_0$ (left side).
I built a program to send a ball down the brachistochrone and compare to other curves as my final school project some years ago.
Here you go:
[](http://tobiasgurdan.de/facharbeit/Brachistochrone/Brachistochrone.html)
Think of particles in a uniform gravitational field (see different coloured points in image below). If they are propagating along a brachistochrone then they will **all reach the end point at the same time independently of their starting positions**.
In this case a **brachistochrone is also something called a tautochrone** (from Greek, taut meaning 'same').
Particles placed near the top will travel faster past the finish line than objects placed near the bottom, but all will finish at the same time. The actual time taken is $$ T = 2\pi \sqrt{\frac{a}{g}},$$ where $a$ is the radius of the cycloid and $g$ the acceleration of gravity.
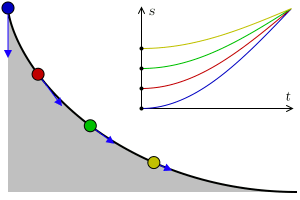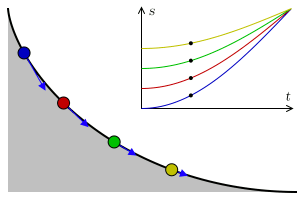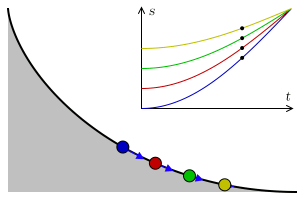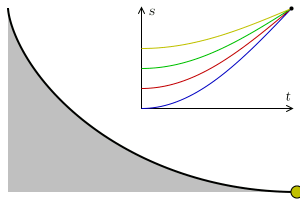
Nice paper.
Recently 3blue1brown did a video on this topic with Steven Strogatz.
Worth checking out:
[](https://www.youtube.com/watch?v=Cld0p3a43fU)
I think this implication only works if we know that $\frac{\partial L}{\partial Y'}$ is finite at $x = x_{1,2}$. That cannot be guaranteed in general, and it doesn't appear to be the case here: we have
\[
\frac{\partial L}{\partial Y'} = \frac{Y'}{\sqrt{2 g Y(Y'^ + 1)}},
\]
which could definitely grow to infinity near $x_{1,2}$ for some choices of $Y$, faster than (some?) choices of $\delta(x)$ go to zero.
There may be some other argument why we can discard this term, but this is not it.
**Brachistochrone** from Ancient Greek βράχιστος χρόνος (brakhistos khrónos) means "shortest time"). In mathematics, a brachistochrone is **the curve of fastest descent**. It is the curve that would carry an object from a starting point at rest and moving along the curve, without friction, under constant gravity, to another end point **in the shortest time**.
Integratio by parts is a theorem that relates the integral of a product of functions to the integral of their derivative and antiderivative. It can be written:
\begin{eqnarray}
\int u(x)v'(x)\,dx=u(x)v(x)-\int v(x)\,u'(x)dx.
\end{eqnarray}
It is easy to derive the author's result (try it!).
You can learn more about integration by parts here: [Wikipedia: integration by parts](https://en.wikipedia.org/wiki/Integration_by_parts)
This problem first introduced the notion of **calculus of variations**. Calculus of variations seeks to find the path, curve, surface for which a function has a stationary value (usually a minimum or maximum). Mathematically, this involves finding stationary values of integrals of the form
\begin{eqnarray}
L = \int{ F(y,y^{\prime},x) \, \mathrm{dx} } \, \, \,,
\end{eqnarray} L has an extreme value only if the following equation is satisfied:
\begin{eqnarray}
\frac{\partial {F}}{\partial{y}} - \frac{\mathrm{d}}{\mathrm{dx}}\frac{\partial {F}}{\partial{y^{\prime}}} =0.
\end{eqnarray}This is the so-called Euler-Lagrange equation.
You can learn more about Euler-Lagrange equations here:
- [Wikipedie: Euler-Lagrange equation](https://en.wikipedia.org/wiki/Euler%E2%80%93Lagrange_equation)
- [Wolfram MathWorld: Euler-Lagrange Differential Equation](http://mathworld.wolfram.com/Euler-LagrangeDifferentialEquation.html)
**The problem of the brachistochrone was formally posed Johann Bernoulli in 1696**. He challenged the scientific community with the following problem:
*Suppose two points A and B lie in a vertical plane, A higher than B but not directly above B. A wire that is bent in the shape of a curve $\gamma$ joins A and B (see figure below). A bead slides along the wire from A to B. There is no force on the bead except the force of gravity; in particular, there is no friction. Find the shape of the curve $\gamma$ that minimizes the time required for the bead to fall from A to B.*
The problem lies not in minimizing the length of the path $\gamma$, but **minimizing amount of time taken to traverse from A to B**.
Figure 1: Decomposition of the gravitational force along the curve $\gamma$.

Bernoulli himself found the solution (using a physical argument partly suggested by Fermat's 'least-time' derivation of Snell's law of refraction in geometrical optics), and Newton had a different proof that it was the correct one. **This problem is widely regarded as the founding problem of the 'calculus of variations' (finding the curve, or surface, minimizing a given integral).**
Galileo Galilei had considered the same problem much earlier. He experimented with objects rolling down tracks of different shapes and commented his finding in a book published in 1638. Galileo showed that a body takes less time to fall along the arc rather than along the chord between two points of a circle. He believed the optimal track would have the shape of a quarter-circle but he did not prove it. We now know that his solution was incorrect, we know that the cycloid is the shape that solves the brachistochrone problem.
Figure 3: This figure shows Galileo's setup when he was studying the Brachistochrone problem.

The cycloid is the path described by a fixed point (figure 1: red point) on a circle of radius $a$ (figure 1: black line), as the circle rolls on a fixed line (think of a point on a bicycle wheel, depicted by the blue line). Taking the line to be the $x$-axis, and choosing as parameter $\theta$ the angle formed by the point with the vertical, we have that the cycloid is described by the parametric equations:\begin{eqnarray*}
x = a\theta−a\sin(\theta),\,\,\,
y=a−a\cos(\theta).
\end{eqnarray*}
Figure 1: The top image describes a cycloid (red line). The bottom images shows how you can create a cycloid going from a fixed point on a circle that is propagating along a straight line.

## Finding the Cycloid
Here the author just introduces a change of variable that corresponds to a cycloid curve. I would like to dive deeper into this result and explain how we can get there.
We are trying to minimize the value of a definite integral over a family of functions. The problem then is to find, among all functions y(x), the one for each T is smallest possible.
The method of Euler-Lagrange applies to 'variational problems' of the following kind. Given a function of three variables f(x,y,p), find the function y(x) satisfying given 'boundary conditions' $y(a) = y_a$, $y(b) = y_b$ for which the integral:
\begin{eqnarray}
F(y) = \int f (x, y(x), y^{\prime}(x))dx
\end{eqnarray}
has the smallest possible value. Clearly the brachistochrone problem is of this form. Euler and Lagrange discovered that the function y(x) achieving the minimum must satisfy a second-order differential equation, the so-called Euler-Lagrange equation:
\begin{eqnarray}
\frac {\partial F}{\partial y} = {\frac {\mathrm {d} }{\mathrm {d} x}}{\frac {\partial F}{\partial y^{\prime}}}
\end{eqnarray}
Applying this to the Brachistochrone problem (and for now we set $\sqrt{2g} = 1$) we obtain:
\begin{eqnarray}
{\frac {\mathrm {d} }{\mathrm {d} x}}{\frac {\partial F}{\partial y^{\prime}}} = \frac{1}{\sqrt{y(1+(y^{\prime})^2 )}} \left( \frac{y^{\prime \prime}}{1+(y^{\prime})^2} - \frac{(y^{\prime})^2 }{2y} \right)
\end{eqnarray}
and:
\begin{eqnarray}
{\frac {\partial F}{\partial y}} = \frac{\sqrt{1+(y^{\prime})^2 }}{2y^{3/2}} .
\end{eqnarray}
With (3) and (4) one can then rewrite (2) as:
\begin{eqnarray}
y^{\prime \prime} = -\frac{1+(y^{\prime})^2 }{2y}.
\end{eqnarray}
The solution of this equation will give the least-time function y(x).
The first step in the solution of the Euler-Lagrange equation for the brachistochrone problem is to reduce it to a first order equation. We have:
\begin{eqnarray}
2yy^{\prime \prime} + 1 +(y^{\prime})^2 = 0,
\end{eqnarray}
and multiplying by $y^{\prime}$:
\begin{eqnarray}
y^{\prime} + 2yy^{\prime}y^{\prime \prime} +(y^{\prime})^3 = 0,
\end{eqnarray}
where we see that the left-hand side of the equation is simply the derivative that can be written:
\begin{eqnarray}
[y + y(y^{\prime})^2]^{\prime} = 0.
\end{eqnarray}
This means that:
\begin{eqnarray}
y + y(y^{\prime})^2 = C.
\end{eqnarray} and thus:
\begin{eqnarray}
\frac{\mathrm {d} y}{\mathrm {d} x} = \sqrt{\frac{C-y}{y}}
,\frac{\mathrm {d} x}{\mathrm {d} y} = \sqrt{\frac{y}{C-y}}.
\end{eqnarray}Here the author just introduces a change of variable that corresponds to a cycloid curve. I would like to dive deeper into this result and explain how we can get there.
We are trying to minimize the value of a definite integral over a family of functions. The problem then is to find, among all functions y(x), the one for each T is smallest possible.
The method of Euler-Lagrange applies to 'variational problems' of the following kind. Given a function of three variables f(x,y,p), find the function y(x) satisfying given 'boundary conditions' $y(a) = y_a$, $y(b) = y_b$ for which the integral:
\begin{eqnarray}
F(y) = \int f (x, y(x), y^{\prime}(x))dx
\end{eqnarray}
has the smallest possible value. Clearly the brachistochrone problem is of this form. Euler and Lagrange discovered that the function y(x) achieving the minimum must satisfy a second-order differential equation, the so-called Euler-Lagrange equation:
\begin{eqnarray}
\frac {\partial F}{\partial y} = {\frac {\mathrm {d} }{\mathrm {d} x}}{\frac {\partial F}{\partial y^{\prime}}}
\end{eqnarray}
Applying this to the Brachistochrone problem (and for now we set $\sqrt{2g} = 1$) we obtain:
\begin{eqnarray}
{\frac {\mathrm {d} }{\mathrm {d} x}}{\frac {\partial F}{\partial y^{\prime}}} = \frac{1}{\sqrt{y(1+(y^{\prime})^2 )}} \left( \frac{y^{\prime \prime}}{1+(y^{\prime})^2} - \frac{(y^{\prime})^2 }{2y} \right)
\end{eqnarray}
and:
\begin{eqnarray}
{\frac {\partial F}{\partial y}} = \frac{\sqrt{1+(y^{\prime})^2 }}{2y^{3/2}} .
\end{eqnarray}
With (3) and (4) one can then rewrite (2) as:
\begin{eqnarray}
y^{\prime \prime} = -\frac{1+(y^{\prime})^2 }{2y}.
\end{eqnarray}
The solution of this equation will give the least-time function y(x).
The first step in the solution of the Euler-Lagrange equation for the brachistochrone problem is to reduce it to a first order equation. We have:
\begin{eqnarray}
2yy^{\prime \prime} + 1 +(y^{\prime})^2 = 0,
\end{eqnarray}
and multiplying by $y^{\prime}$:
\begin{eqnarray}
y^{\prime} + 2yy^{\prime}y^{\prime \prime} +(y^{\prime})^3 = 0,
\end{eqnarray}
where we see that the left-hand side of the equation is simply the derivative that can be written:
\begin{eqnarray}
[y + y(y^{\prime})^2]^{\prime} = 0.
\end{eqnarray}
This means that:
\begin{eqnarray}
y + y(y^{\prime})^2 = C.
\end{eqnarray} and thus:
\begin{eqnarray}
\frac{\mathrm {d} y}{\mathrm {d} x} = \sqrt{\frac{C-y}{y}}
,\frac{\mathrm {d} x}{\mathrm {d} y} = \sqrt{\frac{y}{C-y}}.
\end{eqnarray}
We now perform a change of variable from x to $\theta$, the ngle the tangent to the curve makes with the vertical. We then have that $dx/dy = \tan(\theta)$ and so:
\begin{eqnarray}
\frac{y}{C-y} = \frac{\sin^2(\theta)}{\cos^2(\theta)}
\end{eqnarray} which can be rewritten:
\begin{eqnarray}
y = C\sin^2(\theta).
\end{eqnarray}
We now take the derivative in respect to $\theta$:
\begin{eqnarray}
\frac{\mathrm {d} y}{\mathrm {d} \theta} = 2C \sin(\theta) \cos(\theta),
\end{eqnarray} and we can now rewrite (20) as:
\begin{eqnarray}
\frac{\mathrm {d} x}{\mathrm {d} \theta} &=& \sqrt{\frac{y}{C-y}} \frac{\mathrm {d} y}{\mathrm {d} \theta} \\
&=& 2C \sin^2(\theta) \\
&=& C ( 1 - \cos(2\theta) )
\end{eqnarray} and integrating equation (26):
\begin{eqnarray}
x &=& C \int{ ( 1 - \cos(2\theta) ) d\theta} \\
&=& \frac{C}{2}(2\theta - \sin{2\theta}).
\end{eqnarray}
We have now a set of parametric equations for the solution curve y(x):
\begin{eqnarray}
x = \frac{C}{2}(2\theta - \sin{2\theta}),
\,\,y = \frac{C}{2}(1 - \cos{2\theta}).
\end{eqnarray}
The curve described by these parametric equations is a familiar one: it is the cycloid.
**Thus we found that the Brachistochrone is the Cycloid.**
