### Zero knowledge proofs
A Zero-knowledge proof is a process by...
### Interactive proofs
An interactive proof is a protocol between ...
The thief enters the cave before Ali Baba. The thief chooses to pro...
In Zero-knowledge proofs there is usually some small probability, t...
This section about the simulation of the proof might seem confusing...
(1)
Philips Research Laboratory, Avenue Van Becelaere, 2, B-1170 Brussels, Belgium.
(1)
CCETT/EPT, BP 59, F-35512 Cesson S&ignP, France.
(3)
Anagram Laboratories, P.O. Box 791, Palo Alto CA 94301, USA.
How to Explain Zero-Knowledge Protocols
to Your Children
QUISQUATER Jean-Jacques(‘), Myziam, Muriel, Micha2;1
GUILLOU Louis(‘), Marie AnnicJc, GaicJ, Anna, Gwenoli, Soazig
in collaboration with Tom BERSON’“) for the English version
0 Know, oh my children, that very long ago, in the
Eastern city of Baghdad, there lived
an old man named Ali Baba. Every day Ali Baba would go to the bazaar to buy or sell
things. This is a story which is partly about Ali Baba, and partly also about a cave, a
strange cave whose secret and wonder exist to this day. But I get ahead of myself . . .
One day in the Baghdad bazaar a thief grabbed a purse from Ali Baba who right away
started to run after him. The thief fled into a cave whose entryway forked into two dark
winding passages: one to the left and the other to the right (The Entry of the Cave).
\
Ali Baba did not see which passage the thief r
into. Ali Baba had to choose which way to go, and
he decided to go to the left. The left-hand passage
ended in a dead end. Ali Baba searched all the
way from the fork to the dead end, but he did
not find the thief. Ali Baba said to himself that
the thief was perhaps in the other passage. So he
searched the right-hand passage, which also came
to a dead end. But again he did not find the thief.
. . . . .._........___...........................
“This cave is pretty strange,”
said Ali Baba to himself, “Where has my thief gone?”
The following day another thief grabbed Ali Baba’s basket and fled, as the first thief
had fled, into the strange cave. Ali Baba pursued him, and again did not see which way
the thief went. This time Ali Baba decided to search to the right. He went all the way
to the end of the right-hand passage, but he did not find the thief. He said to himself
that, like the first thief, the second thief had also been lucky in taking the passage Ali
Baba did not choose to search. This had undoubtedly let the thief leave again and to
blend quietly into the crowded bazaar,
The days went by, and every day brought its thief. Ali Baba always ran after the
thief, but he never caught any of them. On the fortieth day a fortieth thief grabbed
Ali Baba’s turban and fled, as thirty-nine thieves had done before him, into the strange
cave. Ali Baba yet again did not see which way the thief went. This time Ali Baba
decided to search the left-hand passage, but again he did not find the thief at the end
of the passage. Ali Baba was very puzzled.
He could have said to himself, as he had done before, that the fortieth thief had
been as lucky as each of the other thirty-nine thieves. But this explanation was so
G. Brassard (Ed.): Advances in Cryptology - CRYPT0 ‘89, LNCS 435, pp. 628-631, 1990.
0 Springer-Verlag Berlin Heidelberg 1990
629
far-fetched that even
Ali
Baba did not believe
it.
The
luck of
the
forty thieves was just
too good
to
be
a matter of chance. There was only one chance
in
a million million that
all of the forty would escape!
So
Ali
Baba
said
to
himself
that there
must
be another
more likely explanation. He began to suspect
that
the strange cave guarded a secret!
And
Ali
Baba set
out
to
discover the secret of the strange cave.
He
decided to hide
under some sacks at the end
of
the right-hand passage.
After a very uncomfortable
wait he saw a thief arrive who, sensing
he
was pursued by his victim, whispered the
magic words, “Open sesame.”
Ali
Baba was amazed to see the wall of the cave slide
open. The thief ran
through
the opening. Then the wall slid closed again. The pursuer
arrived, and was all upset
to
find
only
Ali
Baba under the sacks at the dead end of the
passage. The thief had escaped. But
Ali
Baba was all happy,
for he was
finding
out
the Secret
of
the
Strange Cave.
He
discov-
ered to
his
amazement
that
when the wall
slid
open
the
right-hand passage was connected with the left-hand
passage. Now
Ali
Baba knew how
all
of the forty
Y
Ali
Baba experimented with the magic words.
thieves
had
escaped from him.
AliBaba worked
and
worked with the magic words,
and
he
finally managed to replace them with new
magic words, a
little
like you change the combi-
nation for some padlocks. The very next day a
thief
was caught.
Ali
Baba recorded
this
story and
his
discovery
in
a lovely illuminated manuscript. He did not write down the new magic
words,
but
he included
some
subtle clues about them.
Ali
Baba’s lovely illuminated manuscript aked
in
Italy in
the
Middle Ages. Today
it
is in the United States, near Boston. There
it
has recently
held
the
full
attention of
several curious researchers. Through decryption
of
the
subtle clues, these researchers
have even recovered the new magic words!
After
several archaeological excavations in
the
ruins of
the
old Baghdad bazaar,the
strange cave was located.
It
was not
a
myth!
And,
despite
the
centuries, the magic
words still worked.
All
agog, the curious researchers went through the end wall between
the two passages.
The television networks were quickly made aware of the unusual events taking place
in Baghdad.
A
big
American network even got an exclusive on the story. One of the
researchers, a certain Mick
Ali,
a descendent perhaps of
Ali
Baba, wanted to demon-
strate that he knew the secret.
But
he did not want to reveal
the
secret. Here is what
he
did.
First, a television crew filmed a detailed
tour
of
the
cave with the two dead-end
passages. Then everybody went out of the cave. Mick
Ali
went back in alone and went
down one of the passages. Then the reporter, accompanied by
the
camera, went inside
only as far as the fork. There he flipped a coin to choose between
right
and left.
If
the
coin come
UP
heads he would tell Mick to come out on
the
right.
If
the coin came up
tails he would
tell
Mick to come out on the left.
It
was
heads,
so
the reporter called
630
out loud, “Mick, come
out
on the right.”
And
Mick
did
just that.
In memory of the forty thieves
this demonstration scene was played forty times.
Each of the times everybody went back out of the cave and Mick entered alone all the
way
in
to one of the passages.
Then
the reporter and the camera went as far as the
fork where he chose by flipping a coin which order to give to Mick. Mick succeeded
in
all
forty scenes.
Anybody who
did
not know the secret of
the
cave would have
been
exposed on the
first failure. Each new test divided by two the chances
of
success for someone without
the secret.
On
the other hand, the secret allowed Mick to come out each time by
the
required exit.
Employed by another television network, a jealous reporter wanted to also
film a story
on the strange cave. Mick refused to participate because he had given exclusive rights
to the story to the first network.
But
Mick mischievously suggested to
the
jealous reporter that the story could be
filmed without possessing the secret. The jealous reporter thought and thought, and
finally he understood.
He
said to himself,
“I
even know
a
stage actor who looks like
Mick
Ali
and
who could be mistaken for him.”
And
the second story was
filmed.
In the course
of
the
filming half of the scenes
were spoiled because Mick’s double
did
not know how to
get
from one passage
to
the
other! The jealous reporter edited the tape and only kept the successful scenes until he
had forty of them.
The two stories were broadcast at
the
same hour on the same evening
by
the two
competing American networks. The matter was taken to court. Both videotapes were
placed into evidence.
But
the judges and the experts could not
tell
the tapes apart.
Which tape was simulated? Which tape was
genuine?
The
tapes alone were not enough
to
judge
by.
The simulation surely conveyed
no
knowledge of the secret.
But
the simulation and
the genuine tape were indistinguishable.
So the genuine tape
did
not convey knowledge
of the secret either. The reporter who had gotten the exclusive story had been convinced
at the time that Mick
Ali
knew the secret,
but
the reporter could not pass his conviction
on
to
the judges
in
court
or
to the television audience either.
Mick
Ali
had achieved his real objective. He wanted, in
fact,
to show that
it
is
possible
to
convince without revealing, and
so
without unveiling
his
secret.
Meanwhile, other researchers
in
Israel observed that by using several secrets and making
tests
in
parallel, one could reduce the number of scenes in
the
films.
In
other words,
the length of the authentication.
They imagined an apartment building with one cave per floor, each having
its
own
magic words. They needed was one extra actor per cave.
All
the floors could be filmed
at once to see where the actor came out on each floor.
They even proposed an arithmetic solution where a reply with a single
number
as
proof could replaced many actors.
Still, a compromise between the number
of
secrets and the number
of
scenes
to
63
1
film may not always be optimal.
It
would
be
much better to have a single secret and a
single scene.
Besides
that,
simulation by successive attempts becomes less and less practical
as
the number of secrets increases.
Do
we have
no
conveyance of knowledge when you
cannot simulate with successive attempts?
All
of this really intrigued some European researchers. They made an observation that
applies equally to the serial version and to
the
parallel version.
To
save time filming,
the
jealous reporter and Mick
Ali’s
double would have been pretty clever to
think
of
agreeing
in
advance
on
a
list
of forty random selections between
right
and
left.
During
the filming, the jealous reporter would have then pretended to choose the questions
at
random in
his
head, and the double, who knew in advance the questions he would be
asked,
would not need to know
the
secret and could
still
pass all of
the
tests one after
the
other.
Therefore to the simulation technique of successive attempts where only the
SUC-
cessful scenes are kept was added a simulation technique of prior agreement between
prover and verifier.
In
response
.to
this observation a new cave was set up with more passages ending at
a fork (The Revised Cavq). Certainly the physical construction of the cave becomes
problematic when the number
of
passages increases.
It
is
impossible to build a cave with a million million passages.
But
whatever the number
of
passages, you could sim-
ulate by prior agreement.
A
more arithmetic scheme
would allow a verifier to choose a question from a set
With
a single test
YOU
could directly reach
the
level
of
security obtained with forty
The court is completely unable to tell
the
videotapes apart: one depicting a demon-
stration, the other
a
simulation by prior agreement. Therefore, even when the size of
the
question
is
large the demonstration does not show knowledge of the secret’s value.
c
of
a million million questions.
ccessive tests
in
the cave with two passages.
And
so,
my children, you have heard how
Ali
Baba learned the secret of the strange
cave, and how his descendent, the clever researcher
Mick
Ali,
was able to convince a
television reporter that
he
knew the secret without having to
tell
him what the secret
was. Countless people saw
Mick
Ali
on the television, and
he
became famous and had
adventures around the world. He
still
has not revealed
the
secret
of
the strange cave, but
has convinced many others, including
me,
that
he
does know
it.
The
keeping
of
secrets
reminds
me
of the story of the Merkle Hellrnan and
his
super-increasing knapsack.
But
c300
the hour grows late. That is another story for another time.
Thanks
to
Gilles
Brassard
for
hls
continous interest
and
support.
In the post linked above, there is a soundness error of 1/9. How is this number calculated?
This section about the simulation of the proof might seem confusing but it is worth thinking about.
This concept of simulator is often used to prove that a certain interactive proof is a zero-knowledge proof.
In the simulation, the prover did not know anything about the secret. Yet the the simulated and the genuine transcript (in this case, tape) are indistinguishable to a third party. This means that absolutely no knowledge of the secret can be extracted from the original tape (because that would imply that that same knowledge could be extracted from the simulation, where the prover knew nothing about the secret).
In Zero-knowledge proofs there is usually some small probability, the soundness error, that a cheating prover will be able to convince the verifier of a false statement. However, you can choose to keep decreasing the soundness error to negligibly small values. In this case, all you have to do is run more tests where Mick goes into the cave and exits thru the specified side.
The thief enters the cave before Ali Baba. The thief chooses to proceed in one out of two directions. Then Ali Baba comes into the cave and he is faced with the same choice. If Ali Baba goes in the direction the thief went, then Ali Baba will catch the thief, otherwise, if Ali Baba chooses the wrong direction, the thief will be able to escape before Ali Baba can come back to check the other side of the cave. As a consequence, Ali Baba has a 50% chance of catching the thief each time.
The probability of Ali Baba not catching any of the 40 thieves is:
$$ \left ( \frac{1}{2} \right ) ^{40} = \frac{1}{1.0995116 \cdot 10^{12}}$$
This is an incredibly small number.
### Interactive proofs
An interactive proof is a protocol between two parties in which one party, called the prover, tries to prove a certain fact to the other party, called the verifier. An interactive proof usually takes the form of a challenge-response protocol, in which the prover and the verifier exchange messages and the verifier outputs either "accept" or "reject" at the end of the protocol.
### Zero-knowledge proof properties
- **Completeness** - The verifier will always (eventually) accept the proof if the assertion is true (given both the prover and the verifier follow the protocol)
- **Soundness** - The verifier always rejects the proof if the assertion is false
- **Zero knowledge** - The verifier learns absolutely nothing about the statement being proved (except that it is correct) from the prover that he could not already learn without the prover. This means that, in a zero-knowledge proof, the verifier cannot even later prove the fact to anyone else.
There are some forms of non-interactive zero-knowledge proofs. You can read more about it here ["Non-Interactive Zero-Knowledge and Its Applications”](http://www.dtic.mil/cgi-bin/GetTRDoc?AD=ADA222698)
### Zero knowledge proofs
A Zero-knowledge proof is a process by which one party (the prover) can prove to another party (the verifier) the validity of a given assertion, without conveying any information apart from the fact that the assertion is indeed valid.
Zero-knowledge proofs were first introduced in 1985 by Shafi Goldwasser, Silvio Micali, and Charles Rackoff in their
paper ["The Knowledge Complexity of Interactive Proof-Systems”](https://groups.csail.mit.edu/cis/pubs/shafi/1985-stoc.pdf). Together with a paper by László Babai and Shlomo Moran, this paper invented interactive proof systems, for which all five authors won the Gödel Prize in 1993. Zero knowledge proofs (and interactive proofs in general) turned out to be an incredibly influential concept in computer science with applications in a number of different areas ranging from practical identity schemes to theoretical complexity problems.
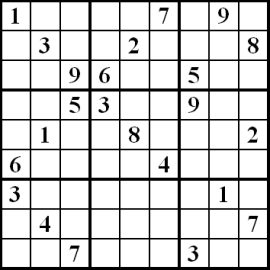
**Zero-knowledge sudoku example**
Imagine I give you the following sudoku puzzle and I tell you I have solved it:
Now, before you give it a try and spend a good deal of time working on it, perhaps you might want me to prove to you that there is indeed a solution for the sudoku problem above. The obvious way for me to prove it would be to just show you the solution - which would be a big spoiler. In a zero knowledge proof, I am able to convince you I know how to solve the sudoku problem, without giving you the solution (if you want to know how to actually do this go [here](http://www.wisdom.weizmann.ac.il/~naor/PAPERS/SUDOKU_DEMO/) ).